Офисные прикладные программы MS Office 2007: Microsoft Excel
Использование тригонометрических функций
Задача 2.3.
Определить, какая сила действует на вмонтированную в пол скобу, если к правому концу веревки, прикрепленной к этой скобе, приложена сила F1 400 Н под углом 20° к горизонтали, а к левому - сила F2 200 Н под углом 45° к горизонтали?
Исходные данные
Сила, и угол, под которым она приложена к правому и левому концу веревки (рис.44).
Модель решения задачи
При решении задач с помощью тригонометрических функций следует помнить, что угол должен быть задан в радианах.
Вертикальные составляющие действующих сил складываются, а горизонтальные - частично компенсируют друг друга, поскольку они направлены в разные стороны (рис.44).
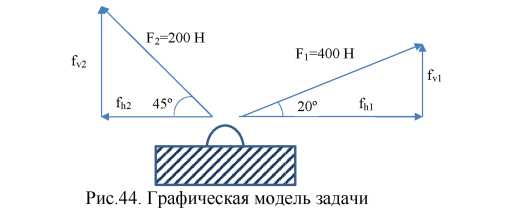
Сила F1 раскладывается на составляющие fv1 и fhl, а сила F2 - на составляющие fv2 и fh2, которые можно вычислить через соответствующие углы по формулам:
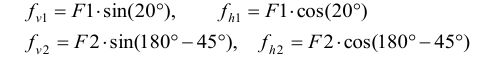
Зная компоненты обеих сил, можно вычислить компоненты результирующей силы: f =fhl +fh2, f,=fv1 +fv2
Тогда результирующую силу, действующую на скобу, и угол ?, под которым она направлена, можно найти по формулам:
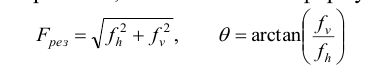
Решение задачи
1. В ячейки В2:ЕЗ вводятся исходные данные (рис.45).
Результат решения задачи представлен на рис.45.
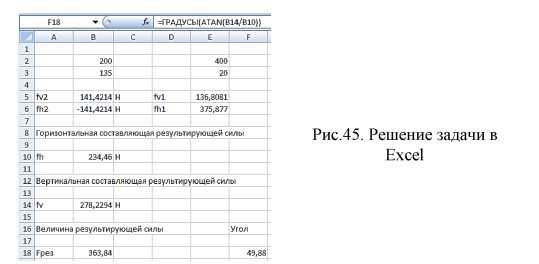
2. Расчетные формулы вводятся в ячейки согласно таблицы 3. (функция РАДИАНЫ () переводит градусы в радианы).
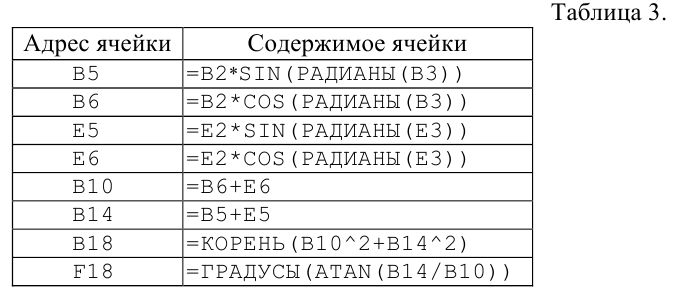
Результат решения задачи представлен на рис. 45.
Задача 2.4.
Тело брошено с начальной скоростью 30 м/с под углом 35° к горизонту (рис.46).

Определить:
" дальность полета (х);
" общее время движения (t);
" время движения до максимальной высоты (tYmax);
" максимальную высоту полета (Ymax);
" угол падения, скорость при падении (Р, vk),
Сопротивлением воздуха можно пренебречь.
Исходные данные
Угол, под которым тело бросили к горизонту, (а), начальная скорость тела (vo), высота начальной точки над уровнем земли (ho), ускорение свободного падения (g).
Модель решения задачи
Вертикальную и горизонтальную составляющие начальной скорости можно выразить через угол: ![]()
Тогда для координат х, у можно записать:
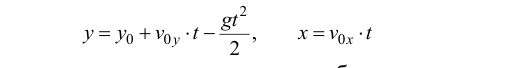
Сопротивлением воздуха можно пренебречь, поэтому проекция скорости тела на горизонтальную ось будет константой, т.е. координата х и есть дальность полета. Так как условие приземления тела у=0, то можно найти время приземления:
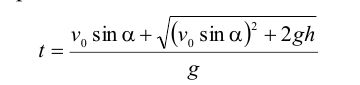
Поскольку движение по вертикали происходит под действием постоянной силы тяжести, то оно является равнозамедленным до достижения верхней точки на траектории и равноускоренным - после нее; движение же по горизонтали является равномерным. Формула равноускоренного движения vy =v0y-gt, а в верхней точке vy=0, то время достижения верхней точки на траектории
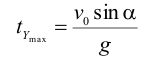
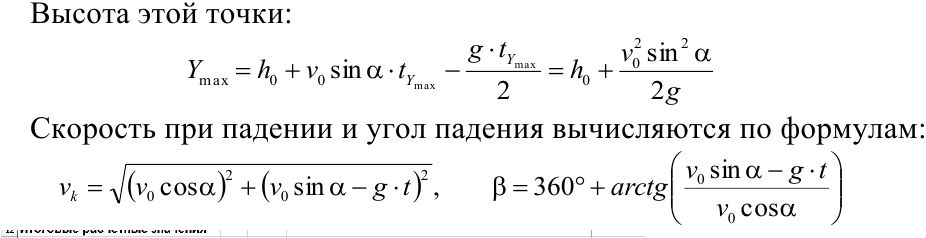
Решение задачи
1. В ячейки G4:G7 вводятся исходные данные (рис.47).

2. Расчетные формулы вводятся в соответствующие ячейки согласно рис.47 (Функция РАДИАНЫ () переводит градусы в радианы).
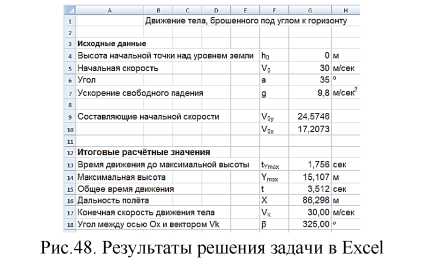
На рис.47 представлен рабочий лист решения задачи в режиме отображения формул, а на рис.48 - результат.
Задача 2.5.
Подготовим традиционную таблицу квадратов двузначных чисел (рис.49), так хорошо знакомую каждому из курса алгебры.

В ячейку А3 введите число 1, в ячейку А4 - число 2, выделите обе ячейки и протащите маркер выделения (+) вниз, чтобы заполнить столбец числами от 1 до 9. Аналогично заполните ячейки В2 - К2 числами от 0 до 9.
После заполнения строчки числами от 0 до 9 оказалось, что не все необходимые для работы ячейки одновременно видны на экране. Их необходимо сузить таким образом, чтобы все столбцы имели одинаковую ширину (чего нельзя добиться, изменяя ширину столбцов мышкой). Для этого, выделив столбцы от А до К, выполните команду Главная - Ячейки-Формат - Ширина столбца и введите значение, например, 5.
В ячейку В3 нужно поместить формулу, которая возводит в квадрат число, составленное из десятков, указанных в столбце А и единиц, соответствующих значению, размещенному в строке 2. Таким образом, само число, которое должно возводиться в квадрат, в ячейке В3 задается формулой =АЗ*10+В2 (число десятков, умноженное на десять плюс число единиц). Остается возвести это число в квадрат.
Для ввода формулы в ячейку В3 воспользуемся Мастером функций. Выделите ячейку, в которой должен разместиться результат вычислений (В3), и вызовите Мастер функций fx, это же окно выводится на экран выбором команды Функция-Библиотека функций-Формулы (рис.50).
В списке Категория перечислены категории, в которые объединены функции. В списке Выберите функцию перечислены функции, относящиеся к выбранном категории. Под списком расположено описание синтаксиса выбранной функции и самой функции. Общее количество функций в Excel очень велико, порядка двухсот сорока. Комбинируя встроенные функций Excel, можно выполнять расчеты любой сложности для любой области применения.

Среди предложенных категорий функций выберите Математические, среди Функций - Степень, закончив действие, нажатием кнопки Ок.
В диалоговом окне Степень (рис.51) введите в поле Число (основание степени) - А3*10+В2 и в поле Показатель степени - 2. Ввод ссылок на адреса ячеек, используемых в формуле, производится с помощью мыши с указанием соответствующих ячеек.
В тех случаях, когда окно ввода прикрывает ячейки необходимые для ввода аргументов, можно свернуть (развернуть) это окно с помощью кнопки ![]() , расположенной справа от поля ввода аргументов. Кроме того, окно Мастера функций можно переместить в сторону, "схватив" мышью за заголовок окна.
, расположенной справа от поля ввода аргументов. Кроме того, окно Мастера функций можно переместить в сторону, "схватив" мышью за заголовок окна.
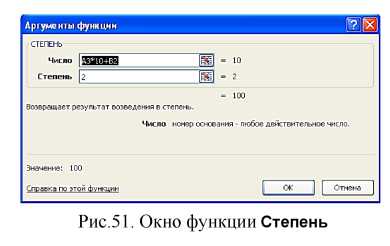
В этом же диалоговом окне (рис. 51) можно увидеть значение самого числа (10) справа от окна ввода аргумента и результат вычисления функции (степени =100) под окнами ввода аргументов.
После ввода аргументов функции (кнопка Ok), в ячейке ВЗ появится результат вычислений.
Для распространения этой формулы на остальные ячейки таблицы, выделив ячейку В3, заполните соседние ячейки с помощью маркера заполнения (черный плюс в нижнем правом углу ячейки). После окончания данного действия получим результат, представленный на рис.52.

Почему результат не оправдал наших ожиданий? В ячейке С3 не видно числа, так как оно не помещается целиком в ячейку.
Расширьте мышью столбец С. Число появилось на экране, но оно явно не соответствует квадрату числа 11 (рис.53).

Дело в том, что когда мы распространили формулу вправо, Excel автоматически изменил адреса ячеек с учетом нашего смещения, на которые ссылается формула, и в ячейке С3 возводится в квадрат не число
а число, вычисленное по формуле =ВЗ*10+С2.
Для получения правильного ответа необходимо вернуть ширину столбца С в исходное положение и выполнить следующие действия:
" Выделить ячейку ВЗ и, установив текстовый курсор в Строку формул, исправить в имеющейся формуле =СТЕПЕНЬ (А3*10+В2; 2) ссылки на ячейки АЗ и В2 с помощью клавиши F4 на $А3 и В$2, получив в итоге формулу =СТЕПЕНЬ ($А3*10+В$2, 2).
" После этого, воспользовавшись услугами маркера заполнения, можно заполнить этой формулой все свободные ячейки таблицы (сначала протянуть маркер заполнения вправо, отпустить левую клавишу мыши, затем, не снимая выделения с полученного блока ячеек, вниз).
Для ввода ссылок на ячейки с данными столбца А и строки 2 были использованы смешанные ссылки, закрепляющие столбец ($А3) и строку (В$2). Абсолютную ссылку в нашем примере можно было бы использовать, если бы в формуле вместо числа 10, на которое умножаются числа в столбце А, использовался бы адрес ячейки, на которую умножались бы эти числа, например, А15 (где ввели бы это число 10). В этом случае формула в ячейке В3 записалась бы в виде: =СТЕПЕНЬ ($А3*$А$15+В$2), а затем была бы скопирована в остальные ячейки. Попробуйте это выполнить.
Осталось оформить таблицу: ввести и ячейку А1 заголовок, отформатировать его и отцентрировать по выделению, выполнить обрамление таблицы и заполнение фоном отдельные ячейки.