Офисные прикладные программы MS Office 2007: Microsoft Excel
Матричные операции в Excel
Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы.
Задача 5.17.
Сложение матриц и умножение матрицы на число. Сложить матрицы м и N, где
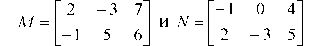
Решение. Введем матрицы M и N в блоки A1:С2 и E1:G2. В блок А4:С5 введем табличную формулу {=А1: С2+Е1: G2}. Обратите внимание, что выделен блок имеет те же размеры, что и исходные матрицы.
Что произойдет, если перед вводом формулы выделить блок А4:D6? В «лишних» ячейках появится #Н/Д, т.е. «НеДоступно». А если выделить А4:В5? Будет выведена только часть матрицы, без каких- либо сообщений. Проверьте.
Использование имен делает процедуру ввода табличной формулы намного проще. Дайте диапазонам A1:С2 и 1:G2 имена M и N соответственно с помощью команды Формулы-Присвоить Имя. В блок Е4:G5 введите табличную формулу {=M+N}. Результат, естественно, должен получиться тот же.
Теперь вычислим линейную комбинацию матриц 2 M-N. В блок А7:С8 введем табличную формулу {=2*M-N}. У Вас должны получиться результаты:
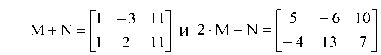
Рассмотренные примеры подводят нас к мысли, что обычная операция умножения применительно к блокам не вполне эквивалентна перемножению матриц. И действительно, для матричных операций в Excel предусмотрены функции, входящие в категорию «Математические»:
- МОПРЕД - вычисление определителя матрицы;
- МОБР - вычисление обратной матрицы;
- МУМНОЖ - перемножение матриц;
- ТРАНСП - транспонирование.
Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как формулы массивов. Первая буква М в названии трех функций - сокращение от слова «Матрица».
Задача 5.18.
Вычислить определитель и обратную матрицу для матрицы
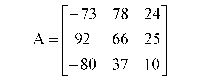
Проверить правильность вычисления обратной матрицы умножением ее на исходную. Повторить эти действия для той же матрицы, но с элементом а33=10,01.
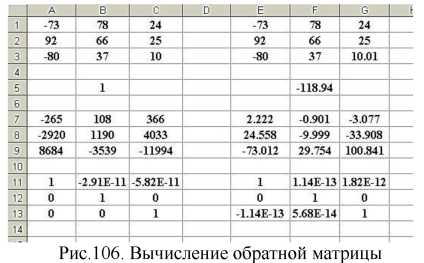
Решение. Разместим исходную матрицу в блоке А1:СЗ (рис. 106).
В ячейке в 5 поместим формулу для вычисления определителя =МОПРЕД(А1:СЗ) .
В блок А7:С9 введем формулу для вычисления обратной матрицы. Для этого, выделив блок А7:С9 (он имеет три строки и три столбца, как и исходная матрица), введем формулу {=МОБР (А1:СЗ)}. Да же если используется
Мастер функций, завершить ввод нужно нажатием комбинации клавиш Shift+Ctrl+Enter (вместо кнопки ОК). Если предварительно не выделив блок А7:С9, ввести формулу в ячейку А7 как обычную формулу Excel (закончив ввод клавишей Enter), то не нужно вводить ее заново на остальной диапазон. Просто выделив А7:С9, выберите F2 (редактирование) и, не изменяя формулу, закончите действие комбинацией клавиш Shift+Ctrl+Enter.
Скопируйте блок А1:С9 в блок E1:G9. Измените один элемент исходной матрицы: в ячейку G3 вместо 10 введите 10,01. Изменения в определителе и в обратной матрице разительны! Этот специально подобранный пример иллюстрирует численную неустойчивость вычисления определителя и обратной матрицы: малое возмущение на входе дает большое возмущение на выходе.
Для дальнейших вычислений присвоим матрицам на рабочем листе имена: А1: СЗ - А, А7 : С9 - Ainv, El: G3 - АР, Е7 : G9 - APinv. Теперь проверим правильность вычисления обратной матрицы. В блок А12 : С14 введем формулу {=МУМНОЖ (A, Ainv) }, а в блок E12:G14 - формулу {=мумнож (ар, APinv) }. У вас должен получиться результат, как на рис. 107.
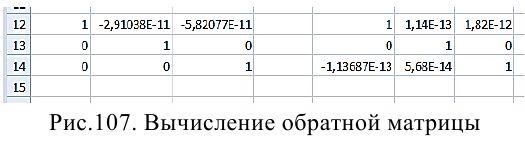
Как и следовало ожидать, получились матрицы, близкие к единичным.