Офисные прикладные программы MS Office 2007: Microsoft Excel
Поиск решения
В занятии 4 мы рассматривали пример автоматического нахождения функциональной зависимости Y=f (х). Напомним, что нахождение подобной зависимости необходимо для предсказания значений отклика
параметра Y на выходе эксперимента от фактора - независимых переменных X на входе в систему.
В некоторых случаях представленных в Excel функций бывает недостаточно. Поэтому важно уметь подобрать такую функцию самостоятельно, используя какой-нибудь из математических методов оптимизации, например, метод наименьших квадратов. Суть его состоит в том, чтобы минимизировать сумму квадрата разности экспериментальных (Уэкпер) и расчетных (YpaC4CT) данных:
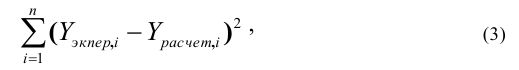
где п в нашей задаче было равно 10.
Скопируйте задачу занятия 4 на новый лист (выделив название листа, из контекстного меню выберите скопировать) и продолжите заполнение таблицы. Экспериментальные Y уже введены, осталось заполнить таблицу расчетными Y.
Для этого нам понадобится дополнительная таблица коэффициентов, начальные значения которых приравняем к 1 (Рис. 108).
Теперь осталось ввести формулу полинома второй степени
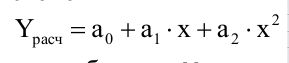
в столбец для Yрасчет.
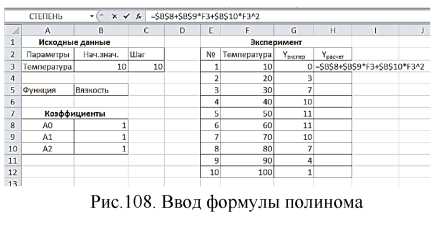
Далее задача заключается в том, чтобы подобрать коэффициенты уравнения таким образом, чтобы разница между Yрасчет и Yэкспер была минимальной. Для оценки точности нашего расчета вводится функция расчета суммы квадрата разности (3) и формула расчета критерия Пирсона (Рис. 109). Обе формулы являются встроенными в Excel и являются примером функций, для которых можно обойтись без ввода табличных формул (Занятие 5).
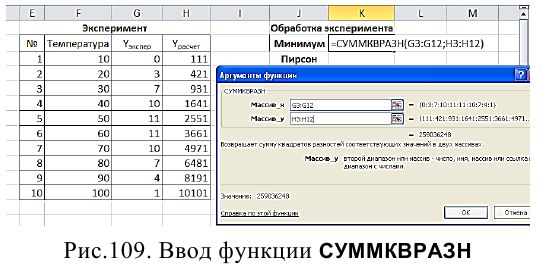
Открыв Мастер функций (fx), в категории «Математические» выберите формулу СУММКВРАЗН и закончите, выбрав ОК. В открывшемся окне в качестве массива_х введите массив Yэкспер, в качестве массива_у - массив Yрасчет и нажмите ОК.
Формула для расчета критерия Пирсона находится в категории «Статистические» (функция PEARSON). Во втором окне Мастера функций в качестве массива_х также введите массив Yэкспер, в качестве массива_у - массив Yрасчет и нажмите ОК.
Для подбора значений коэффициентов, в Excel имеется надстройка Поиск решения, которая позволяет решать задачи отыскания наибольших и наименьших значений, а также решать различные уравнения.
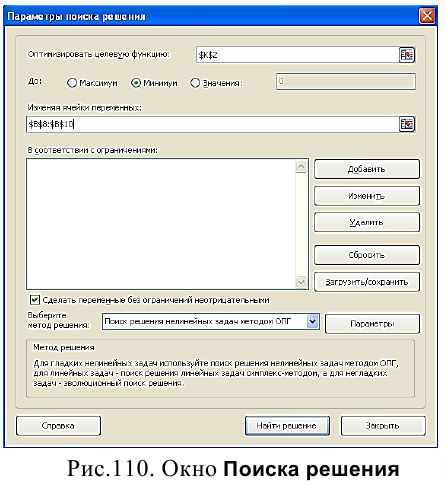
Выделив ячейку с формулой расчета квадрата разности, выполните команду Данные – Анализ - Поиск решения. В открывшемся окне Поиск решения (Ошибка! Источник ссылки не найден.110) введите следующие параметры:
- в поле Оптимизировать целевую функцию ввести адрес целевой ячейки с подбираемым значением (адрес ячейки с формулой суммы квадрата разности), если ячейка заранее выделена, то адрес помещается автоматически;
- в поле До установите переключатель Минимум;
- в поле Изменяя ячейки переменных введите диапазон ячеек изменяемых коэффициентов.
Кнопка Параметры служит для изменения и настройки параметров поиска. В их число входят: способ решения задачи, время проведения вычислений и точность результатов. Однако в большинстве случаев достаточно использовать настройки по умолчанию. Поиск решения осуществляется после щелчка по кнопке Выполнить.
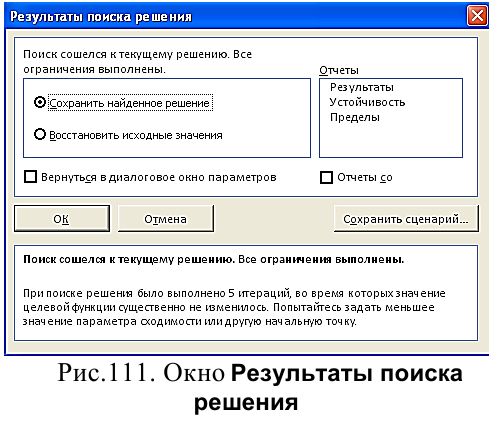
Если поиск решения успешно завершен, то результаты вычислений заносятся в исходную таблицу, а на экране появляется диалоговое окно Результаты поиска решения (Рис. 111), с помощью которого можно сохранить найденные решения в исходной таблице, восстановить исходные значения, сохранить результаты поиска решения в виде сценария, сформировать отчет по результатам выполнения операции поиска решения.
Поскольку поиск решения является итерационным процессом ее сходимость может быть достигнута не сразу. Если удовлетворительной точности не достигнуто с первой попытки, операцию поиска решения можно повторить.
Сравните полученные значения коэффициентов с коэффициентами в уравнении линии тренда.
Добавьте расчетные значения Y на график. Для этого перейдите в окно диаграммы, щелкните правой кнопкой мыши в любом ее месте и выберите в контекстном меню команду Исходные данные. В открывшемся диалоговом окне Выбор источника данных (Рис. 112) выберите кнопку Добавить.
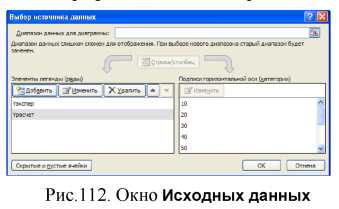
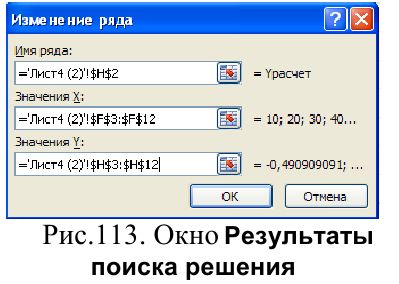
В поле Имя ряда щелкните по кнопке свертывания окна 
, перейдите на лист с вашими данными, выделите ячейку заголовка столбца Ypасчет и вернитесь в окно с помощью кнопки разворачивания окна Я1. Аналогичным образом введите Значения X (диапазон ячеек со значениями X или температуры) и Значения Y (диапазон ячеек со значениями расчетного Y). По окончании ввода нажмите кнопку ОК (Рис. 113).
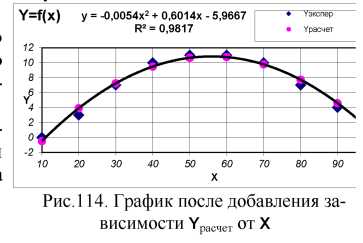
Обратите внимание, что точки Yрасчет легли на линию тренда, построенную нами ранее (Рис. 114).
В завершение обязательно сохраните свой файл, мы будем его использовать на следующем занятии 7.
